Controlling Chaotic Turbulence: Creating ‘Cat-Coat’ Patterns in Fluids

Have you ever stood by a river with rapids and gazed at them as they rushed past you? If so, you would have seen chaotic motion up close and personal, and such motion is better known as turbulence.

“In the natural world, we can encounter turbulence in the atmospheres of stars, but the most characteristic example is that of turbulence in fluids, such as a flowing river,” says Xander de Wit, PhD researcher in the Department of Applied Physics and Science Education. “Turbulence might be commonplace in nature, but it is still only partially understood in science.”

An eddy cascade

Zoom in on a turbulent fluid, and you’ll find an array of vortices, also known as eddies, of all sizes, whose evolution has a lot to do with the dynamics of energy.

“Large eddies can be created by putting energy into a fluid at large scale. Just think of shaking a bottle of water,” says Federico Toschi, professor at the Department of Applied Physics and Science Education. “After some time, the large eddies in the bottle of water break up to form smaller eddies, that in turn produce even smaller eddies in a cascade, leading to eddies of vastly different sizes in the fluid.”

The transfer of energy from large eddies to small eddies is better known as a direct or forward cascade, which stops once the energy has been dissipated by the fluid viscosity at the smallest scale. In a fluid, viscosity describes how a fluid resists changes to its structure or flow.

With turbulent flows so intricately linked to chaos, it seems to be unfounded, and somewhat confusing, to consider making regular patterns from the chaotic motion of turbulent flows.

Well, this is exactly what de Wit and Toschi explored and modelled via computer simulations in collaboration with Michel Fruchart, Tali Khain, and Vincenzo Vitelli from the University of Chicago as outlined in a new paper in Nature.

Meet odd viscosity

So, a direct or forward cascade sees large eddies produce smaller eddies. But to explore how patterns could be formed in fluids, the researchers needed to input energy at the smallest length scales and then have it transferred to the larger length scales.

“Turbulence in 2D and rotating flows can transfer energy from small to larger scales in a process known as an inverse cascade,” notes de Wit. “So, we looked at the case where a fluid experiences both a direct (transfer of energy from large to small) and inverse cascade (transfer of energy from small to large).”

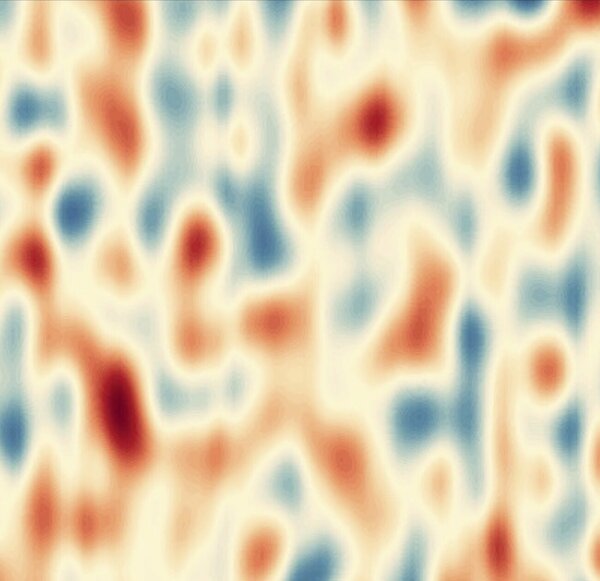
But, to generate patterns in a fluid experiencing both direct and inverse energy cascades, the researchers needed to turn to a special type of viscosity that does not dissipate energy known as odd or Hall viscosity.

“With the inclusion of odd viscosity, we were able to create a new turbulent flow state that has never been studied before,” says Toschi.

Thanks to the inclusion of odd viscosity and some variations in the effect of odd viscosity, the researchers created spot-like patterns in flows that look like the pattern in the fur of a tabby cat, and less like conventional turbulent flows.

“The two cascades – direct and inverse – were found to balance at a certain length scale and that’s where the patterns we describe in the Nature paper emerged, such as the tabby cat pattern,” adds de Wit.

The need for lots of computers

However, for the researchers to investigate pattern formation in turbulent fluids, they needed the right computational resources.

“Simulating turbulence in 3D flows in general is a daunting problem due to the computational costs involved,” says Toschi. “This is because turbulence is something that emerges due to physical processes over varying periods of time, and over small and large sizes.”

In fact, the smallest features in a turbulent flow can be more than 1,000 times smaller than the largest features in terms of both their size and the time over which they evolve. “Modeling this information at these scales requires a lot of computational power,” adds de Wit. “The special odd viscous properties of the fluid also meant that we had a larger computational cost than for the standard turbulence modeling that we normally do.”

To solve the problem, the researchers developed very efficient computer programs, and critically, they turned to supercomputers to solve the Navier-Stokes equations (a set of equations to describe how a fluid moves) for turbulent flows.

So, the researchers used more than 3 million CPU hours, which is the equivalent of running 1,000 modern laptops for more than 15 days non-stop, to solve the turbulent flow equations with the computational resources made available by SURFsara, which is the national supercomputing facility in the Netherlands.

Smart excitement

There are several instances in the natural world where the turbulent behavior studied by the researchers can be observed, but the odd viscosity needs to be quite high for these to happen.

“These special and extreme conditions could be achieved in astrophysical systems, or in quantum systems,” says de Wit. “For instance, it’s believed that patterns in solar winds develop from the mechanisms explored in this study.”

The researchers in Eindhoven and Chicago are looking to the future, with excitement about what might lie ahead now that they understand how order emerges from chaos in turbulent flows.

“We want to be surprised in the future. And we’re hoping this will be the case,” says de Wit. “Next up, we will work on designing laboratory experiments to explore how to control or shape turbulence using smart particles.”