MIT-developed Flexible Solution Aids Artists in Enhancing Animation
Artists who bring to life heroes and villains in animated movies and video games could have more control over their animations, thanks to a new technique introduced by MIT researchers.
Their method generates mathematical functions known as barycentric coordinates, which define how 2D and 3D shapes can bend, stretch, and move through space. For example, an artist using their tool could choose functions that make the motions of a 3D cat’s tail fit their vision for the “look” of the animated feline.
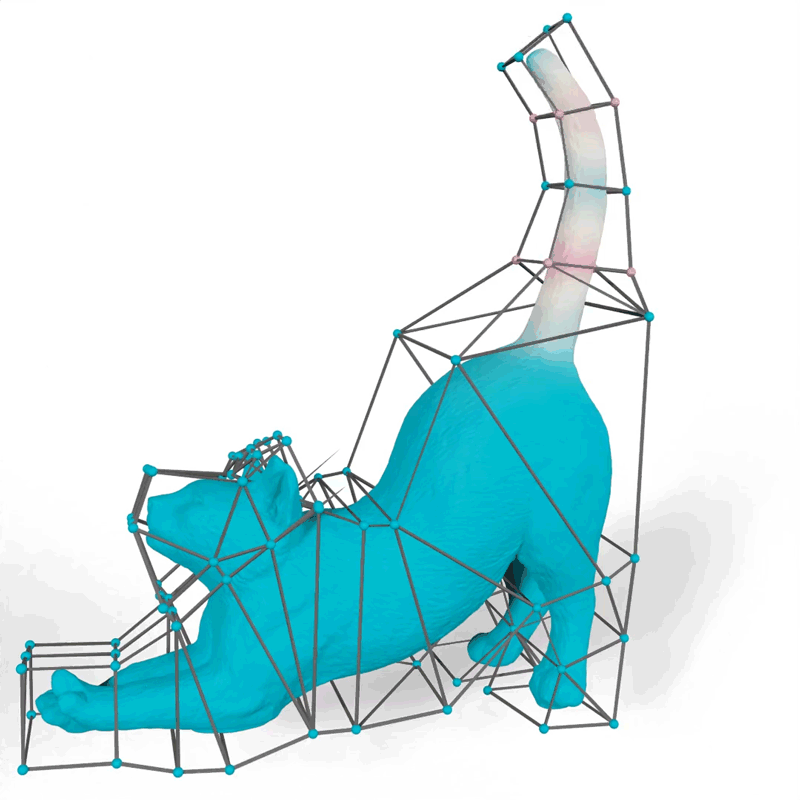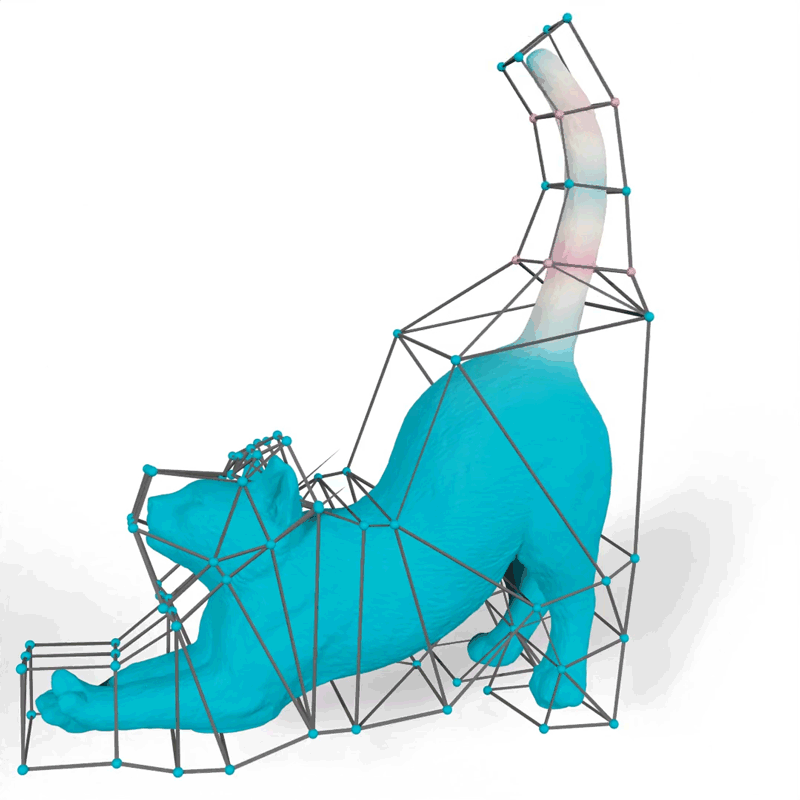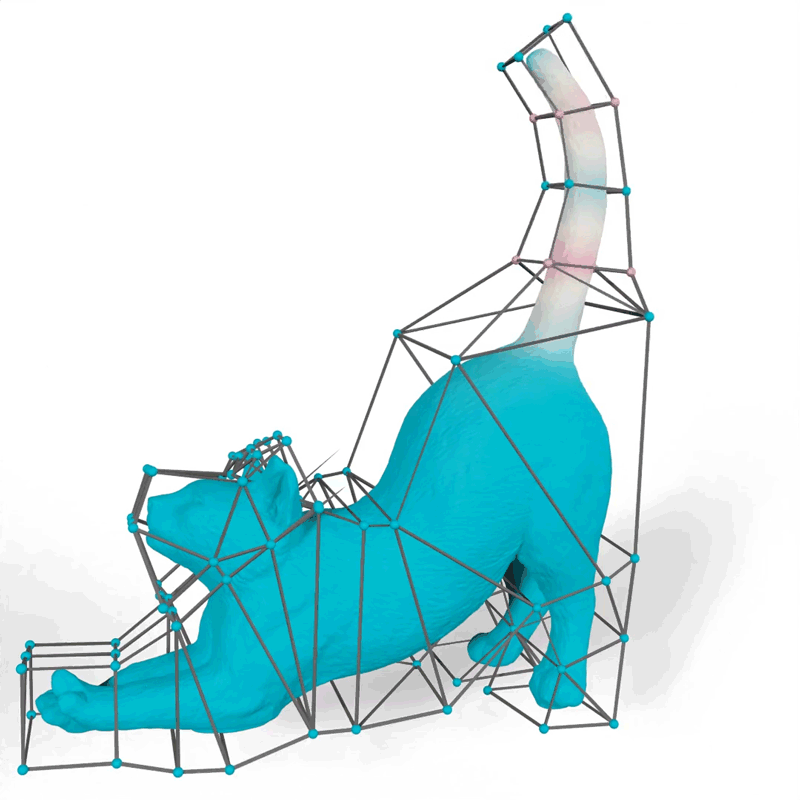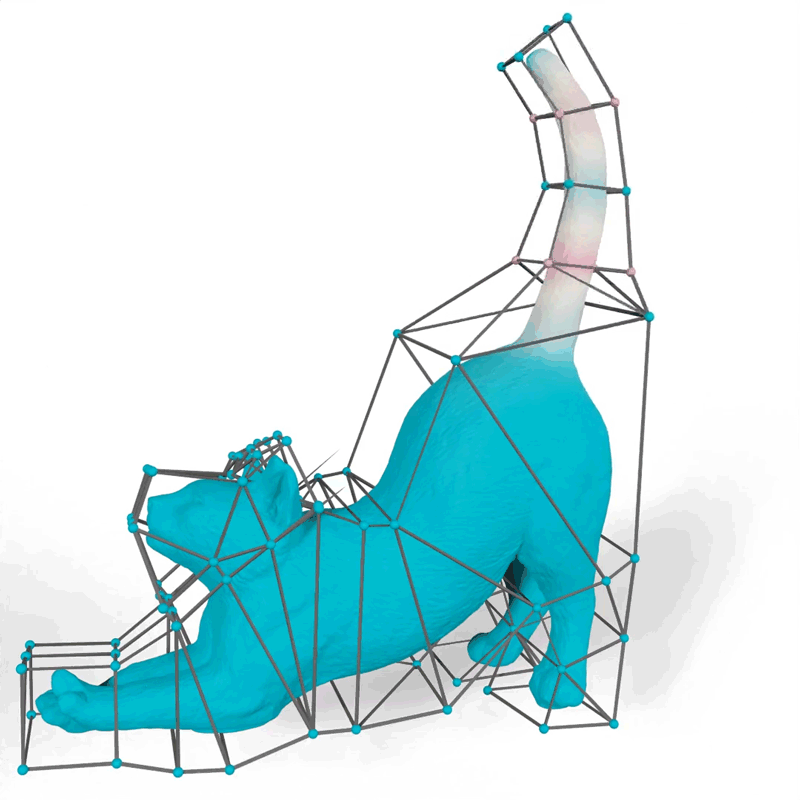
Image: Courtesy of the researchers
Many other techniques for this problem are inflexible, providing only a single option for the barycentric coordinate functions for a certain animated character. Each function may or may not be the best one for a particular animation. The artist would have to start from scratch with a new approach each time they want to try for a slightly different look.
“As researchers, we can sometimes get stuck in a loop of solving artistic problems without consulting with artists. What artists care about is flexibility and the ‘look’ of their final product. They don’t care about the partial differential equations your algorithm solves behind the scenes,” says Ana Dodik, lead author of a paper on this technique.
Beyond its artistic applications, this technique could be used in areas such as medical imaging, architecture, virtual reality, and even in computer vision as a tool to help robots figure out how objects move in the real world.
Dodik, an electrical engineering and computer science (EECS) graduate student, wrote the paper with Oded Stein, assistant professor at the University of Southern California’s Viterbi School of Engineering; Vincent Sitzmann, assistant professor of EECS who leads the Scene Representation Group in the MIT Computer Science and Artificial Intelligence Laboratory (CSAIL); and senior author Justin Solomon, an associate professor of EECS and leader of the CSAIL Geometric Data Processing Group. The research was recently presented at SIGGRAPH Asia.
A generalized approach
When an artist animates a 2D or 3D character, one common technique is to surround the complex shape of the character with a simpler set of points connected by line segments or triangles, called a cage. The animator drags these points to move and deform the character inside the cage. The key technical problem is to determine how the character moves when the cage is modified; this motion is determined by the design of a particular barycentric coordinate function.
Traditional approaches use complicated equations to find cage-based motions that are extremely smooth, avoiding kinks that could develop in a shape when it is stretched or bent to the extreme. But there are many notions of how the artistic idea of “smoothness” translates into math, each of which leads to a different set of barycentric coordinate functions.
The MIT researchers sought a general approach that allows artists to have a say in designing or choosing among smoothness energies for any shape. Then the artist could preview the deformation and choose the smoothness energy that looks the best to their taste.
Although flexible design of barycentric coordinates is a modern idea, the basic mathematical construction of barycentric coordinates dates back centuries. Introduced by the German mathematician August Möbius in 1827, barycentric coordinates dictate how each corner of a shape exerts influence over the shape’s interior.
In a triangle, which is the shape Möbius used in his calculations, barycentric coordinates are easy to design — but when the cage isn’t a triangle, the calculations become messy. Making barycentric coordinates for a complicated cage is especially difficult because, for complex shapes, each barycentric coordinate must meet a set of constraints while being as smooth as possible.
Diverging from past work, the team used a special type of neural network to model the unknown barycentric coordinate functions. A neural network, loosely based on the human brain, processes an input using many layers of interconnected nodes.
While neural networks are often applied in AI applications that mimic human thought, in this project neural networks are used for a mathematical reason. The researchers’ network architecture knows how to output barycentric coordinate functions that satisfy all the constraints exactly. They build the constraints directly into the network, so when it generates solutions, they are always valid. This construction helps artists design interesting barycentric coordinates without having to worry about mathematical aspects of the problem.
“The tricky part was building in the constraints. Standard tools didn’t get us all the way there, so we really had to think outside the box,” Dodik says.
Virtual triangles
The researchers drew on the triangular barycentric coordinates Möbius introduced nearly 200 years ago. These triangular coordinates are simple to compute and satisfy all the necessary constraints, but modern cages are much more complex than triangles.
To bridge the gap, the researchers’ method covers a shape with overlapping virtual triangles that connect triplets of points on the outside of the cage.
“Each virtual triangle defines a valid barycentric coordinate function. We just need a way of combining them,” she says.
That is where the neural network comes in. It predicts how to combine the virtual triangles’ barycentric coordinates to make a more complicated, but smooth function.
Using their method, an artist could try one function, look at the final animation, and then tweak the coordinates to generate different motions until they arrive at an animation that looks the way they want.
“From a practical perspective, I think the biggest impact is that neural networks give you a lot of flexibility that you didn’t previously have,” Dodik says.
The researchers demonstrated how their method could generate more natural-looking animations than other approaches, like a cat’s tail that curves smoothly when it moves instead of folding rigidly near the vertices of the cage.
In the future, they want to try different strategies to accelerate the neural network. They also want to build this method into an interactive interface that would enable an artist to easily iterate on animations in real time.
This research was funded, in part, by the U.S. Army Research Office, the U.S. Air Force Office of Scientific Research, the U.S. National Science Foundation, the CSAIL Systems that Learn Program, the MIT-IBM Watson AI Lab, the Toyota-CSAIL Joint Research Center, Adobe Systems, a Google Research Award, the Singapore Defense Science and Technology Agency, and the Amazon Science Hub.

