Tokyo Institute of Technology Advances Optimization of Continuous-Variable Functions with Quantum Annealing
Quantum annealing (QA) can be competitive to classical algorithms in optimizing continuous-variable functions when running on appropriate hardware, show researchers from Tokyo Tech. By comparing the performance of QA running on a D-Wave quantum computer to that of state-of-the-art classical algorithms, they find that a sufficient suppression of thermal noise can enable QA to significantly outperform classical algorithms.
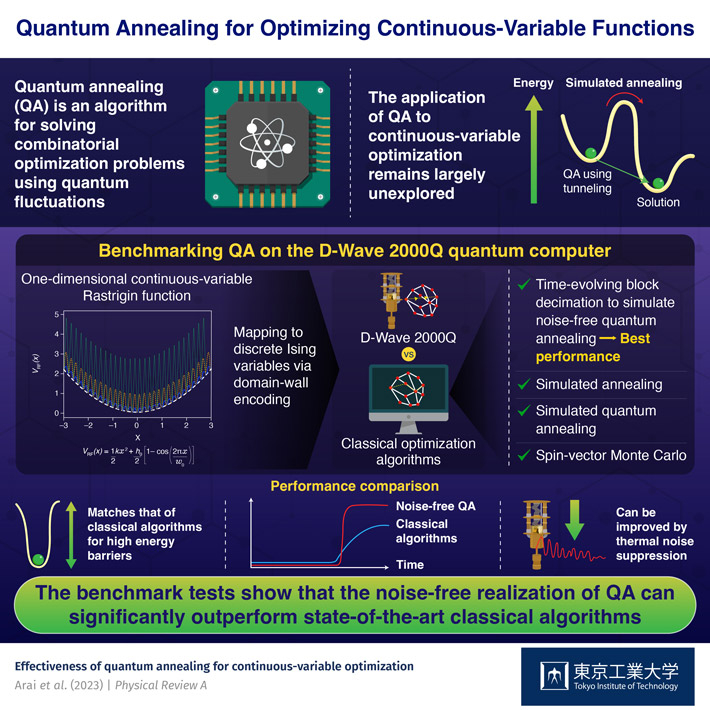
Quantum annealing (QA) is a cutting-edge algorithm that leverages the unique properties of quantum computing to tackle complex combinatorial optimization problems (a class of mathematical problems dealing with discrete-variable functions). Quantum computers use the rules of quantum physics to solve such problems potentially faster than classical computers. In essence, they can explore multiple solutions to a problem simultaneously, giving them a significant speed advantage for certain tasks over classical computers. In particular, QA harnesses the phenomenon of “quantum tunneling,” where particles can “tunnel” through energy barriers without the requisite energy to cross over them, to find solutions for combinatorial optimization problems.
Up until now, QA has almost exclusively been used to solve discrete-variable functions (functions that have discrete-valued variables). The potential of QA for optimizing continuous-variable functions has remained largely unexplored.
Against this backdrop, a team of researchers from Japan, Shunta Arai and Hidetoshi Nishimori from Tokyo Institute of Technology (Tokyo Tech) and Hiroki Oshiyama of Tohoku University, has recently tested the continuous-variable optimization performance of QA on the D-Wave 2000Q quantum computer and compared the results with those by classical algorithms. Their findings were published in the journal Physical Review A.
“We systematically investigated whether QA has an advantage over classical algorithms by optimizing the Rastrigin function, a one-dimensional continuous function used as a standard for benchmarking optimization algorithms,” explains Prof. Nishimori. The team used a technique called “domain-wall encoding” to map a continuous variable to discrete Ising variables and performed two sets of benchmark tests.
The team first compared the performance of QA on the D-Wave 2000Q to that of several state-of-the-art optimization algorithms designed for continuous-variable functions, such as Nelder-Mead, conjugate gradient descent, basin-hopping, and differential evolution, all of them running on classical computers. They found that, for higher energy barriers, D-Wave performed as well or even better than the classical algorithms, albeit only for a limited time range. For longer execution times, the classical algorithms performed better, while D-Wave plateaued off.
In the second part of their study, the team compared the performance of D-Wave with classical discrete-variable optimization algorithms: simulated annealing (SA), simulated QA (SQA), and spin-vector Monte Carlo (SVM). They also included the time-evolving block decimation (TEBD) algorithm, which simulates noise-free coherent QA on a classical computer. Notably, the performance of all algorithms except TEBD, which outperformed the rest, was found to be dependent on the energy barrier height, a dependence natural for SA, SQA and SVM.
Crucially, the dependence of D-Wave QA on barrier height implies that its performance is affected by thermal noise in the hardware and can, therefore, be significantly improved by minimizing the noise and other hardware imperfections.
Prof. Nishimori highlights, “Classical algorithms would struggle to find a solution if the energy barrier becomes even higher than what we tested, while QA, if realized coherently, would be far less affected.” These results suggest that with optimized hardware, QA can significantly outperform state-of-the-art classical algorithms, even for optimizing continuous functions.
Overall, this study thus represents a significant step toward systematic and quantitative studies of continuous-variable optimization by QA compared to a range of well-established classical algorithms.

